Motion planning for multiple robots is a challenging task. When numerous robots occupy the same space, it becomes essential to efficiently compute their trajectories while adhering to kinematic and formation constraints. The objective is to enable multiple robots to reach their respective destinations while avoiding collisions with each other.
The research team from Harbin Institute of Technology proposed a novel centralized trajectory generation method and validated the algorithm's efficiency, adaptability, and scalability through real experiments using the NOKOV motion capture system. The paper was recognized at the International Conference on Intelligent Robots and Systems (IROS) in 2021.
Figure 1: search page
Algorithm Principles
The methods for multi-robot motion planning can be divided into two main categories:
Firstly, distributed methods achieve collective behavior through local interactions between neighboring robots, requiring low communication and offering strong scalability. However, it is challenging to impose constraints at the individual or system level.
On the other hand, centralized methods can provide global guarantees and reasonably set constraint conditions, but their scalability often diminishes as the number of robots increases.
The research team extended the well-known motion planning method GPMP2 to multi-robot scenarios, using sparse Gaussian process models to efficiently compute the trajectories of multiple robots.
By adding formation constraint conditions, the multi-robot formation can adaptively navigate through continuously changing terrain. Additionally, an incremental replanning algorithm was proposed, utilizing Bayesian trees to update motion trajectories, allowing for quick wireless operation.
Experimental Procedures
The research team conducted experiments using a group of quadcopter drones to test the algorithm framework.
The experiments were conducted with three common scenarios in mind: maintaining formation, replanning for changing destinations, and adaptively changing formations when passing through spaces of varying widths.
A set of Crazyflie nano quadcopter drones were monitored by the NOKOV motion capture system during the experiments. Via the CrazyRadio PA system, the drones received positioning data directly from the NOKOV motion capture system.
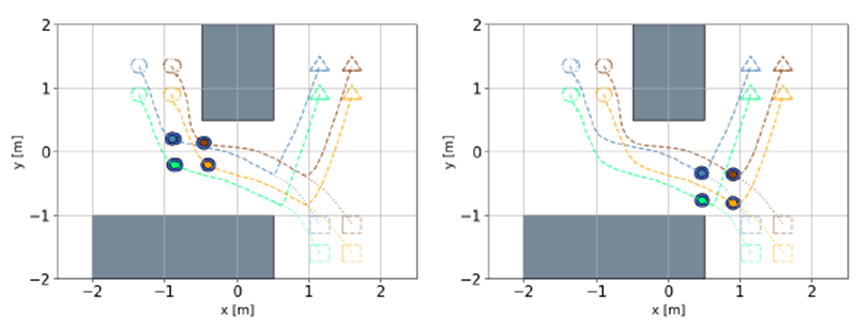
Figure 2: Snapshots of experiment 1 and experiment 2 running trajectories taken at 2.4 and 7.0 seconds. The original target is marked as a square, and the new target is a triangle.
Experiment 1 and 2: Maintaining formation, changing destination and re-planning route
In Experiment 1, four quadcopters maintained a square formation while flying towards a target. The formation may adjust when necessary to avoid obstacles. A slight distortion occurs in the formation through turns but allowed for smoother turns overall.
In Experiment 2, as the quadcopter formation flew towards a target, the target point was suddenly changed. At t = 7s, the target point was moved in the direction opposite to the original target. The incremental re-planning algorithm updated the trajectory to the new target within 4ms, meeting real-time requirements.
Experiment 3: Adaptive formation change in space with varying width
Six quadcopters pass through spaces of three different widths: 2.5m, 1.5m, and 3.5m. The different formations and execution time intervals calculated by the global planning algorithm are as follows: (i) 1s−2s: 3×2 arrangement; (ii) 4s−7s: 2×3 arrangement; (iii) 9s−10s: 6×1 arrangement.
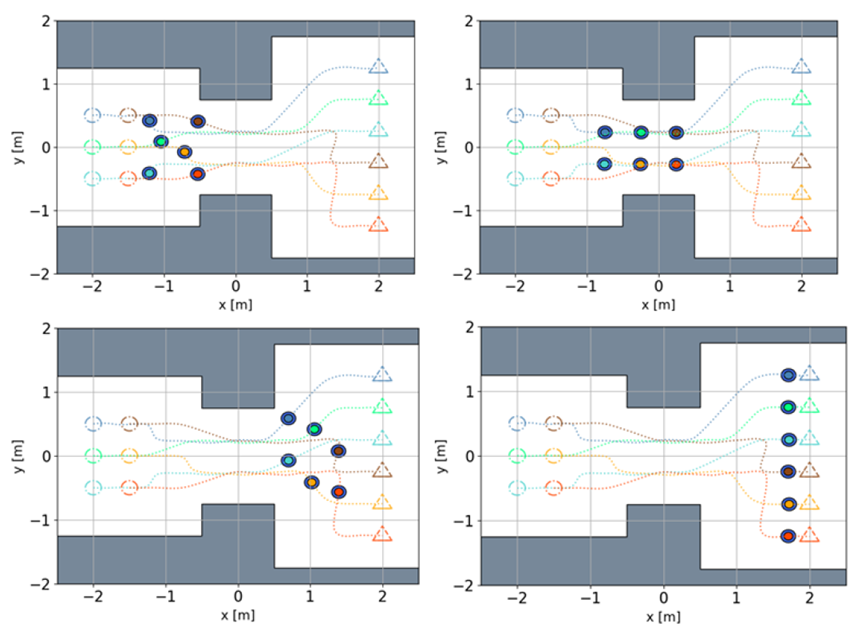
Figure 3: Snapshots at 2.4, 4.0, 7.4 and 9.0 seconds of the six quadcopters changing formation.
Additionally, on a four-layered map, 10 quadcopters passed through spaces of widths: 4m, 2m, and 7m, respectively. The corresponding formations were: (i) 1s−2s: 5 × 2; (ii) 4s−7s: 2 × 5; (iii) 9s−10s: 10 × 1.
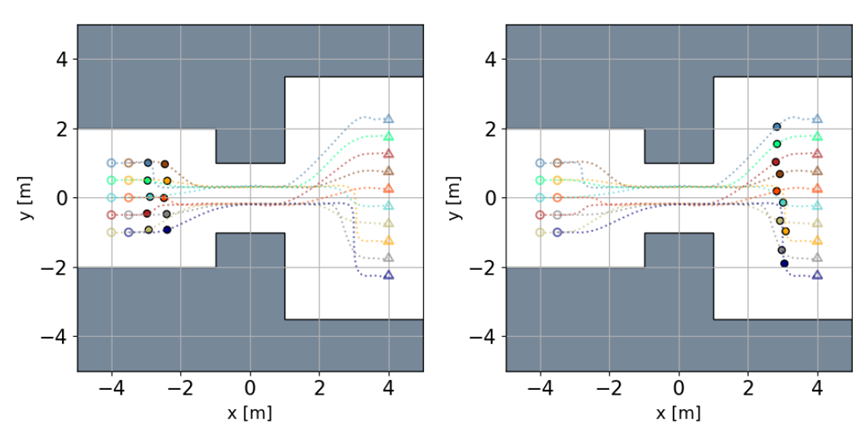
Figure 4: Snapshots at 2.0 and 8.0 seconds of the ten quadcopters changing formation.
Algorithm runtime
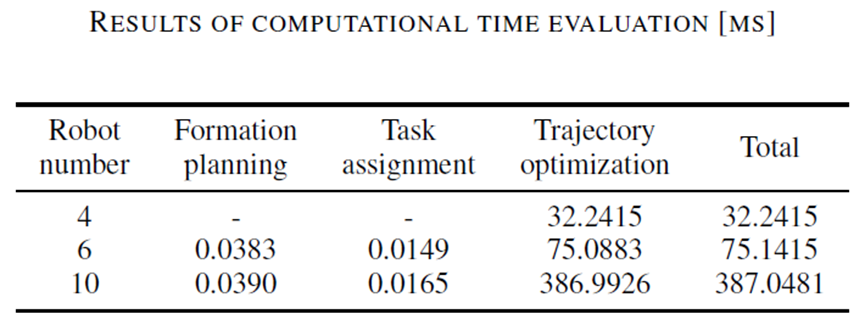
Algorithm runtime
The algorithm was able to compute the complete trajectory for 10 quadcopters within 0.39 seconds, including formation changes, which is highly efficient for such a complex task.
Bibliography:
Please Feel Free to Reach Us
-
We are dedicated to assisting you with your inquiries and providing comprehensive information.
Share your concerns with us, and we will promptly guide you towards the most effective solution.
-
-
-
- Capture Volume * m m m
-
Objectives to be Tracked *
- Number of Objectives (optional)
-
Camera Type (optional)
-
Camera Count (optional)
- Submit